1 KI – eine neue mathematische Autorität?

1.1 Einleitung

Diese beiden Situationen wirken auf den ersten Blick banal. Sie passieren seit Jahrzehnten im Mathematikunterricht. Und doch zeigen sie etwas Zentrales:

Im Mathematikunterricht vertrauen wir ständig Wissensquellen – oft, ohne es bewusst zu reflektieren.

1.1.1 Was bedeutet „epistemisch"?

Der Begriff „epistemisch" stammt vom griechischen Wort epistēmē und bedeutet „Erkenntnis" oder „gesichertes Wissen". Wenn wir von epistemischem Vertrauen sprechen, geht es um das Vertrauen in eine Wissensquelle: Wem oder was trauen wir zu, zuverlässiges Wissen zu liefern?

Im Mathematikunterricht ist dieses Vertrauen unverzichtbar. Schülerinnen und Schüler können nicht jede Aussage permanent neu beweisen. Sie müssen sich darauf verlassen können, dass bestimmte Quellen grundsätzlich korrekt sind – etwa das Schulbuch, die Lehrkraft oder ein technisches Werkzeug.

Wichtig ist jedoch: Epistemisches Vertrauen ist niemals blindes Vertrauen. Es ist immer an Bedingungen geknüpft und muss dort enden, wo Überprüfung notwendig ist.

1.1.2 Klassische epistemische Vertrauensquellen

Typische epistemische Vertrauensquellen im Mathematikunterricht sind:

• das Schulbuch,
• die Lehrkraft,
• der Taschenrechner oder ein CAS,
• die eigene Rechnung.

Alle diese Quellen sind hilfreich. Keine von ihnen ist unfehlbar. Mathematische Bildung bedeutet deshalb immer auch: prüfen, hinterfragen, begründen.

1.1.3 Die neue Situation: KI

In den letzten Jahren ist eine weitere Wissensquelle hinzugekommen: KI-basierte Sprachmodelle. In diesem Buch identifizieren wir KI grundsätzlich mit generativen Sprachmodellen, auch Large Language Models (LLM) genannt. Typische Vertreter sind ChatGPT oder Gemini, Claude oder DeepSeek (die Liste lässt sich beliebig fortsetzen).

Diese Systeme erzeugen Antworten, die sprachlich souverän, strukturell vertraut und formal korrekt wirken. Sie ähneln damit auf den ersten Blick etablierten Vertrauensquellen wie Schulbüchern oder Musterlösungen.

Der entscheidende Unterschied: KI übernimmt keine epistemische Verantwortung. Sie prüft nicht, ob eine Rechnung stimmt, sofern man sie nicht explizit dazu zwingt. Sie kann richtige und falsche Lösungen gleichermaßen überzeugend formulieren.

Genau daraus ergibt sich eine neue Herausforderung für den Mathematikunterricht.

1.2 Leitfrage dieses Kapitels

Ist KI dabei, im Klassenzimmer als neue mathematische Autorität wahrgenommen zu werden? Falls ja, ist dieses Vertrauen überhaupt gerechtfertigt?

Um diese Frage zu beantworten, lohnt ein genauer Blick auf die Funktionsweise solcher Systeme und auf die Gründe, warum gerade Mathematik für sie besonders fehleranfällig ist.

Wenn diese Systeme in der Lage sind, komplexe Texte zu verstehen, kreative Geschichten zu schreiben und Code zu generieren – warum haben sie dann ausgerechnet mit Mathematik, einem Bereich klarer Regeln und eindeutiger Wahrheitswerte, erhebliche Schwierigkeiten?

Dieses Kapitel beleuchtet die technischen und konzeptionellen Gründe für diese Limitationen und erklärt, warum ein Verständnis dieser Problematik für den erfolgreichen Einsatz im Unterricht unerlässlich ist. In Kapitel 2 werden Sie sehen, dass einige der genannten Probleme mit modernen Systemen (ab 2025) deutlich besser gelöst werden können. Das grundsätzliche Risiko beim blinden Vertrauen ändert das aber nicht.

Die Erklärungen sind kein technischer Selbstzweck. Ziel ist es, Lehrkräften ein realistisches mentales Modell davon zu geben, was KI im Mathematikunterricht leisten kann – und was nicht. Erst dieses Verständnis ermöglicht einen verantwortungsvollen, didaktisch sinnvollen Einsatz.

1.3 Grundlegende Architektur: Autoregressive Sprachmodelle vs. formales Denken

In diesem Buch geht es ausschließlich um LLMs ohne Zusatzmodule. Das ist auch immer gemeint, wenn von „KI" gesprochen wird.

Large Language Models basieren auf der Transformer-Architektur und sind fundamental als autoregressive Sprachmodelle konzipiert. Das bedeutet: Sie erzeugen Text Token für Token, wobei jedes neue Token auf Basis aller vorherigen Tokens vorhergesagt wird (und den Eingabeprompt sowie die vorangegangene Ausgabe umfasst). Dieser Prozess ist im Kern statistischer Natur – das Modell berechnet Wahrscheinlichkeitsverteilungen über mögliche nächste Tokens basierend auf Mustern, die es während des Trainings aus riesigen Textkorpora gelernt hat.

Mathematisches Denken funktioniert jedoch fundamental anders:

• Formales Schlussfolgern: Mathematik beruht auf logischer Deduktion, bei der aus Axiomen und bereits bewiesenen Sätzen neue Aussagen streng abgeleitet werden. Jeder Schritt muss zwingend korrekt und begründbar sein.
• Symbolische Manipulation: Algebraische Umformungen, das Lösen von Gleichungen oder die Differentiation folgen präzisen Regeln, die auf der syntaktischen Struktur mathematischer Ausdrücke basieren.
• Exakte Berechnungen: Numerische Werte müssen präzise verarbeitet werden. Ein Rechenfehler in Schritt 3 einer zehnschrittigen Berechnung macht das Endergebnis wertlos.
• Abstraktion und Generalisierung: Mathematisches Denken erfordert die Fähigkeit, von konkreten Beispielen zu abstrahieren und allgemeine Prinzipien zu erkennen.

Ein LLM „denkt" nicht in diesem Sinne – es erzeugt Text, der mathematischen Aussagen ähnelt, indem es Muster repliziert. Es hat keine interne Repräsentation von mathematischer Wahrheit oder Falschheit.

Für ein grundlegendes Verständnis ist es notwendig zu verstehen, wie Large Language Models eigentlich ihre Eingabe und Ausgabe vornehmen. Sie „lesen" Texte anders als Menschen: Wörter, Zahlen und Satzzeichen werden zunächst in kleinere Einheiten, sogenannte Tokens, zerlegt. Jedem Token wird dann ein Vektor in einem hochdimensionalen Raum (typischerweise mit einigen tausend Dimensionen) zugeordnet. Diese Vektoren, auch „Embeddings" genannt, werden während des Trainings so angepasst, dass sie semantische und syntaktische Beziehungen zwischen Tokens kodieren.

Nach dieser Umwandlung in Embeddings verarbeitet das eigentliche neuronale Netz (meist ein Transformer) die Vektoren in vielen Schichten. In diesen Schichten berechnet das Modell mithilfe von Aufmerksamkeitsmechanismen, welche Tokens für das jeweils nächste Token besonders wichtig sind. Am Ende jeder Vorhersagestufe erhält man eine Wahrscheinlichkeitsverteilung über alle möglichen nächsten Tokens, aus der dann nach bestimmten Strategien (z.B. Auswahl des wahrscheinlichsten Tokens oder zufällige Auswahl aus mehreren Möglichkeiten) das nächste Token gewählt wird. Durch die wiederholte Anwendung dieses Schritts entstehen Wort für Wort bzw. Token für Token ganze Antworten oder Texte.

1.4 Das Problem der Tokenisierung in mathematischen Kontexten

Die Tokenisierung stellt für mathematische Inhalte eine besondere Herausforderung dar. Moderne LLMs verwenden teilwort-basierte Tokenisierung (z.B. Byte-Pair Encoding, BPE), die für natürlichsprachigen Text optimiert ist. Bei mathematischer Notation führt dies zu mehreren Problemen:

1.4.1 Ineffiziente Zahlenrepräsentation

Mehrstellige Zahlen wurden oft in unvorhersehbare Token-Sequenzen zerlegt. Die Zahl '123456' könnte beispielsweise als '12' + '34' + '56' oder '123' + '45' + '6' tokenisiert werden, je nach Trainingsdaten des Tokenizers. Dies hat weitreichende Konsequenzen:

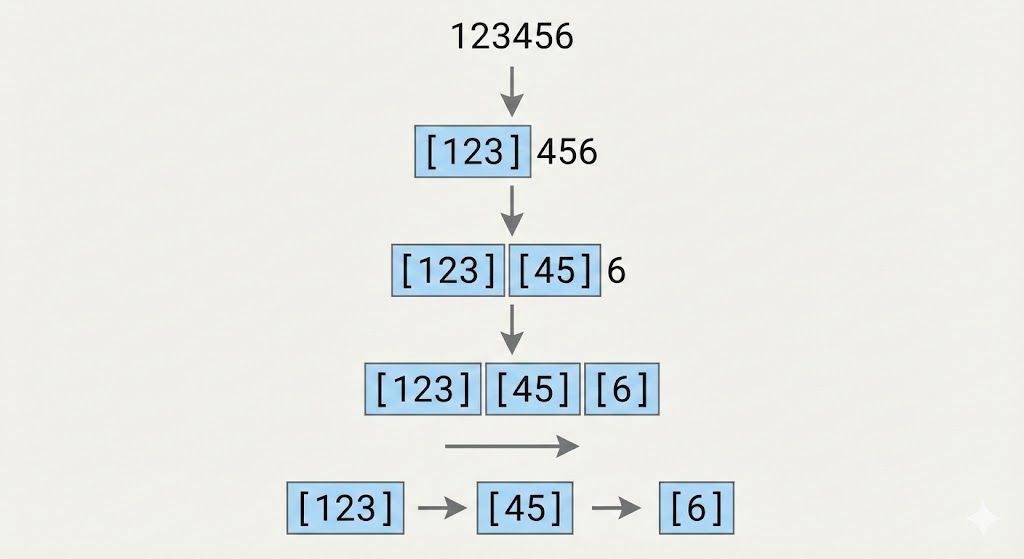
• Arithmetische Operationen werden erschwert, da das Modell die Stellenwerte nicht direkt „sieht", sondern aus der Token-Sequenz rekonstruieren muss.
• Große Zahlen (etwa bei Zinseszinsberechnungen oder exponentiellen Wachstumsprozessen) werden besonders problematisch, da sie in viele Tokens zerfallen.
• Dezimalzahlen und ihre Präzision sind schwer zu kontrollieren, was bei numerischen Aufgaben zu Ungenauigkeiten führt.

1.4.2 Symbolische Notation und Unicode

Mathematische Symbole (∫, ∑, √, ≤, ∈, etc.) werden als einzelne Unicode-Zeichen kodiert, die wiederum in Byte-Sequenzen zerlegt werden. Ein Integral-Symbol '∫' könnte in mehrere Tokens fragmentiert werden, obwohl es semantisch eine unteilbare Einheit darstellt. Besonders problematisch wird dies bei:

• Hochgestellten und tiefgestellten Zeichen (x², aₙ), die für Potenzen und Indizes fundamental sind
• Brüchen in Unicode-Notation (½, ⅓, ¾), die anders tokenisiert werden als ihre LaTeX-Äquivalente (\frac{1}{2})
• Griechischen Buchstaben (α, β, π, Σ), die in der Mathematik spezifische Bedeutungen haben, aber wie 'fremde' Zeichen behandelt werden

1.4.3 LaTeX-Code-Fragmentierung

LaTeX ist die Standardnotation für komplexe mathematische Ausdrücke und wird von den meisten AI-Chatbots unterstützt. Jedoch wird LaTeX-Code wie normaler Text tokenisiert:

1.5 Rechenschwäche und numerische Ungenauigkeit

Ein besonders auffälliges Problem bei den ersten LLMs war ihre Schwäche bei arithmetischen Operationen. Während Menschen (und Computer mit symbolischen Rechensystemen) einfache Rechenoperationen zuverlässig durchführen können, machten LLMs bei Aufgaben wie '347 × 286' oder '1.234.567 + 987.654' häufig Fehler.

1.5.1 Warum konnten LLMs nicht einfach rechnen?

Die Unfähigkeit zu rechnen hat mehrere Ursachen:

1. Token-basierte Verarbeitung: Wie oben erläutert, sehen LLMs Zahlen nicht als numerische Werte, sondern als Token-Sequenzen. Die Multiplikation '347 × 286' wird nicht durch einen Algorithmus berechnet, sondern das Modell versucht, die 'wahrscheinlichste' Fortsetzung des Texts '347 × 286 =' vorherzusagen.
2. Fehlende interne Arithmetikeinheit: Im Gegensatz zu Taschenrechnern oder Computer-Algebra-Systemen (CAS) haben LLMs keine dedizierte Komponente für exakte Berechnungen. Alle Verarbeitung geschieht durch neuronale Netzwerke mit kontinuierlichen Gewichten, die von Natur aus musterbasiert oder approximativ arbeiten.
3. Trainingsverteilung: LLMs wurden anfänglich fast ausschließlich auf Textkorpora trainiert, in denen mathematische Berechnungen zwar vorkommen, aber nicht systematisch für alle möglichen Zahlenkombinationen. Das Modell hat '2 + 2 = 4' millionenfach gesehen, aber '347 × 286 = 99.242' vermutlich nie oder nur sehr selten.
4. Stellenwert und Übertrag: Schriftliche Multiplikation oder Addition mit Übertrag erfordern Zwischenschritte, die in strikter Reihenfolge abgearbeitet werden müssen. Diese sequentielle Abhängigkeit widerspricht der parallelen Verarbeitung in Transformer-Architekturen.

1.6 Fehlende konzeptionelle Verständnis mathematischer Strukturen

Über die technischen Limitationen hinaus fehlt LLMs ein tiefes konzeptionelles Verständnis mathematischer Strukturen. Sie können Muster in mathematischen Texten erkennen und replizieren, ohne die zugrunde liegenden Konzepte zu „verstehen". Daran hat sich bis heute nichts Wesentliches geändert.

1.6.1 Syntaktische vs. semantische Verarbeitung

LLMs operieren primär auf der syntaktischen Ebene:

• Sie erkennen, dass nach '∫' üblicherweise ein Ausdruck und dann 'dx' folgt, ohne zu 'wissen', dass dies eine Integration bedeutet.
• Sie können die Struktur '(a+b)² = a² + 2ab + b²' reproduzieren, weil sie diese Formel häufig gesehen haben, nicht weil sie die binomische Formel 'verstehen'. Tauscht man Termteile aus, ist dieses Muster nur mit deutlich höherem Aufwand zu erkennen.
• Sie generieren Beweisschritte, die oberflächlich korrekt aussehen, aber logische Lücken oder Zirkelschlüsse enthalten können.

1.6.2 Kein „Vorstellungsvermögen"

Sicher ist es Ihnen auch schon aufgefallen: bei Geometrieaufgaben versagen LLMs regelmäßig. Auch hier liegt der Grund wieder in der Systemarchitektur.

Das fundamentale Problem: KI "sieht" nicht

Was ein Mensch tut (räumliches Denken):

Wenn Sie die Aufgabe lesen: "Ein Würfel hat die Kantenlänge 4 cm. Schneide ihn diagonal von einer Ecke zur räumlich gegenüberliegenden Ecke durch. Welche Form hat die Schnittfläche?"

Ihr Gehirn:

• Visualisiert einen dreidimensionalen Würfel
• Rotiert ihn mental, um die gegenüberliegende Ecke zu finden
• Stellt sich vor, wie das Messer durch den Würfel schneidet
• Sieht die entstehende Schnittfläche (ein Rechteck)
• Erkennt die Form visuell

Ein LLM hingegen analysiert Sprachmuster:

Das Modell hat:

• ✗ Keinen Würfel "gesehen"
• ✗ Keine Diagonale "gezogen"
• ✗ Keine Form "erkannt"
• ✓ Nur Wort-Korrelationen aus Trainingsdaten reproduziert

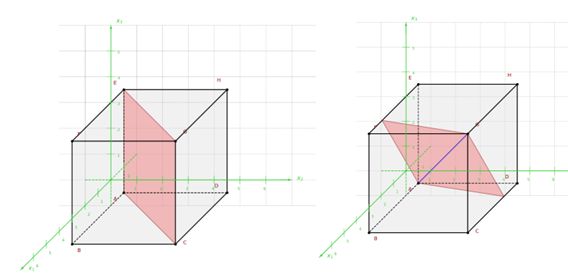
Interessanterweise täuscht auch die menschliche Intuition, da wir uns gerne Spezialfälle vorstellen. Die Schnittebene kann aber um die Raumdiagonale rotieren, dann ergeben sich Parallelogramme. Aber, wie man leicht überlegen kann, niemals ein gleichseitiges Dreieck.

Typische KI-Fehler in Geometrie-Aufgaben

Aufgabentyp	Warum KI versagt	Beispiel-Fehler
Würfelnetze	Kann nicht mental falten	Sagt: "Netz passt", obwohl zwei Flächen sich überlappen würden
Schrägbilder	Kein Konzept von Perspektive	Verkürzt falsche Kanten oder vergisst Hilfslinien
Schnittflächen	Keine 3D-Visualisierung	Verwechselt Kreis und Ellipse bei schrägem Schnitt durch Zylinder
Spiegelungen	Kein räumliches Koordinatensystem	Spiegelt an falscher Achse bei komplexer Formulierung

1.7 Didaktischer Ausblick: Lernen an ungeprüften Lösungen

Als die KI-Welle zunächst in Form von KI-gelösten Hausaufgaben an die Schulen schwappte, sahen das Mathematiklehrkräfte ebenso neidisch wie entspannt:

• Ein klar erkennbarer Mehrwert für den Unterricht wie z.B. bei den Fremdsprachen war zunächst nicht erkennbar
• Die Antworten der ersten LLM-Modelle zu mathematischen Aufgaben waren so unzuverlässig, dass sie für Schülerinnen und Schüler in diesem Fach uninteressant waren.

Folgerichtig befassten sich die ersten didaktischen Vorschläge, KI überhaupt im Mathematikunterricht einzusetzen, meist mit Varianten des Critical Thinkings – entlarven typischer „Denkfehler" von KI durch Schülerinnen und Schüler.

Dieser Ansatz ist weiterhin gerechtfertigt, jedoch sollte man sich weniger auf simple Rechenfehler konzentrieren als auf die unkritische Übernahme scheinbar plausibler Lösungsvorschläge, die kritisch betrachtet nicht „zu Ende gedacht" wurden.

Konkretes Beispiel

Gegeben ist die folgende Gleichung: √x + 5 = x − 1.

Eine KI liefert dazu die folgende Lösung:

Die Lösung wirkt vollständig, formal korrekt und vertraut. Genau so würde sie häufig auch an der Tafel entstehen.

Und doch ist sie falsch.

Der Fehler liegt nicht im Rechnen und nicht in der Umformung. Er liegt in einem fehlenden Schritt: der notwendigen Probe nach dem Quadrieren.

Setzt man die beiden gefundenen Werte in die Ausgangsgleichung ein, ergibt sich:

• x = 4: √9 = 3 ✔
• x = −1: √4 = 2 ≠ −2 ✘

Die zweite Lösung ist eine Scheinlösung und muss verworfen werden.

Dieses Beispiel ist didaktisch aufschlussreich. Die KI hat nicht falsch gerechnet. Sie hat korrekt umgeformt. Was fehlt, ist etwas anderes: die Verantwortung, das Ergebnis zu überprüfen.

Genau hierin liegt die zentrale Herausforderung beim Einsatz von KI im Mathematikunterricht. KI-Systeme erzeugen plausible mathematische Sprache, übernehmen aber keine epistemische Verantwortung für deren Gültigkeit. Diese Verantwortung verbleibt beim Menschen.

Gerade deshalb kann der bewusste Einsatz ungeprüfter oder fehlerhafter KI-Lösungen ein wertvolles didaktisches Instrument sein. Nicht, um Fehler zu provozieren, sondern um mathematisches Urteilen, Prüfen und Begründen gezielt zu trainieren.

Kleine Randnotiz: Überraschenderweise haben gerade fortgeschrittene Modell größere Schwierigkeiten damit, „absichtlich" Lösungen mit Fehlern zu produzieren. Nicht selten ist die Lösung vollkommen korrekt, wird aber trotzdem als fehlerhaft deklariert.

1.8 Zusammenfassung und Implikationen für die Unterrichtspraxis

Die technischen Limitationen von LLMs in Bezug auf Mathematik sind fundamental und nicht bloß temporäre Schwächen, die durch größere Modelle überwunden werden. Sie ergeben sich aus der grundlegenden Architektur:

1. Token-basierte Verarbeitung eignet sich schlecht für symbolische Mathematik
2. Autoregressive Textgenerierung unterscheidet sich fundamental von formalem mathematischem Schließen
3. Fehlende Arithmetikeinheit macht exakte numerische Berechnungen unmöglich
4. Syntaktische Muster ersetzen nicht semantisches Verständnis mathematischer Konzepte
5. Keine Vorstellung führt zu Fehlern bei Geometrieaufgaben

Für die Unterrichtspraxis bedeutet dies:

• Kritische Überprüfung: Alle LLM-generierten mathematischen Inhalte müssen von der Lehrkraft fachlich verifiziert werden. Blindes Vertrauen ist unangebracht.
• Geeignete Einsatzgebiete: LLMs eignen sich besser für die Generierung von Aufgabenideen, didaktischen Texten und Variationen bekannter Aufgabentypen als für komplexe Berechnungen oder Beweise.
• Hybride Ansätze: Kombination von LLMs mit CAS (Computer-Algebra-Systemen) oder anderen spezialisierten Werkzeugen kann Limitationen abmildern.
• Transparenz: Schülerinnen und Schüler sollten über die Grenzen von KI-Systemen aufgeklärt werden, um unkritische Nutzung zu vermeiden. Sie sollten das Überprüfen gezielt üben.

1.8.1 Häufige Missverständnisse (FAQ)

Der folgende Prompt zeigt auf, wo eine händische Prüfung sinnvoll sein kann, insbesondere wenn man eher „schwächere Modelle" verwenden muss oder will. Er dient aber eher der Veranschaulichung und ist heute bei modernen Systemen nicht mehr sinnvoll.

Die folgenden Kapitel bauen auf diesem Verständnis auf und zeigen, wie trotz dieser Limitationen LLMs gewinnbringend im Mathematikunterricht eingesetzt werden können – vorausgesetzt, man kennt ihre Schwächen und arbeitet bewusst damit.